Andreas Atteneder

Matrix Decomposition in Unity

TL;DR: Unity's Matrix4x4.rotation and Matrix4x4.lossyScale deliver incorrect results on some corner-cases. Here's an alternative solution.

In this article I'll tell you about the journey from detecting the problem towards solving it but won't go into math details. Feel free to jump ahead to the problem definition and the solution.

The Issue

A while ago an issue was raised which observed strange rotation errors when loading a glTF 3D assets in Unity with glTFast and I could reproduce it:

"3D scene showing a car in Unity with incorrect rotations on some objects"

Some objects like tires, doors and head lights are rotated incorrectly ☹️. In order to draw comparison (and rule out content errors) I viewed the file in the glTF Viewer and imported it into Blender. In both cases it seemed to work fine:

"3D scene showing a car in Blender with correct rotations and the transform values of the tire object"

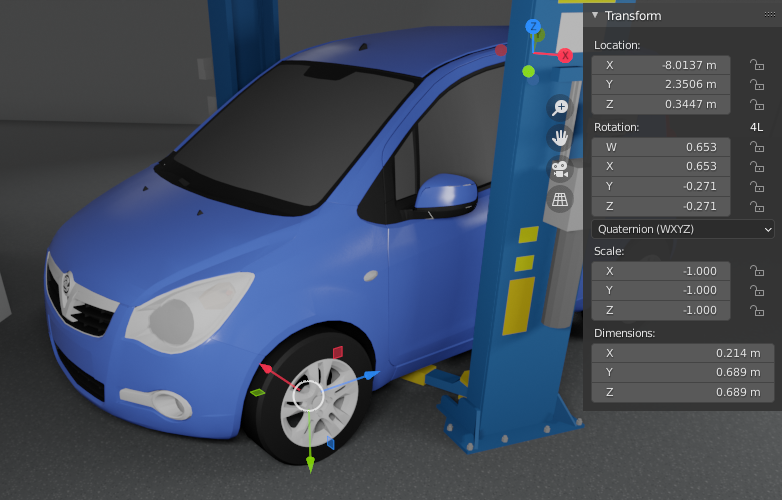
What's cool in Blender is that you can inspect and compare the transform values. I picked one of the tires to inspect closer. If you look at the transform panel (on the right side in the image), you notice that the scale is a uniform negative 1. While that's not good practice, it certainly shouldn't break positioning of objects. The rotation is shown as quaternion. I switched it to Euler, so it's easier to compare it with Unity inspector's transform component.

"Transform values of the tire object with rotation as XYZ euler angles"

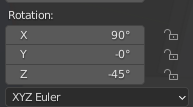
Let's compare this to the transform values in Unity:

"Transform component of the tire object in Unity"

They differ! Even when considering that Unity and Blender have different coordinate systems (Y-up versus Z-up), in Unity…

Let's found out why!

Lucky guess

In the past I rarely had problems with glTF files exported from Blender, so I re-exported the asset and imported this second version in Unity again. This time it worked, so I started comparing the original and the Blender export. glTF's scene definition is JSON based and thus readable.

In glTF, a node's transformation can be defined by either a tuple of translation, rotation, and scale or a (4-by-4) transformation matrix. It turned out the original was using matrices only and the re-export separate transformations 💡.

Enter the Matrix

I decided to dig down into the matrix import code, which consists of two steps:

  1. Convert the matrix from glTF's coordinate space into Unity's (by flipping signs on certain values)
  2. Decomposing the matrix into separate translation, rotation, and scale (since you cannot assign a full matrix to a Unity Transforms).

I tinkered with the space conversion without any luck. I tried a different approach (via conversion matrix multiplication), which yielded the same result as before but didn't solve the issue.

I then wanted to see if omitting the space conversion yielded in the desired uniform scale of -1, which it didn't. I started to suspect the error lies in the matrix decomposition, which looked something like this:

// Given is a matrix (already converted to Unity space):
Matrix4x4 m;

if(m.ValidTRS()) {
  // Translation is the first three values in the last column
  position = new Vector3( m.m03, m.m13, m.m23 );
  rotation = m.rotation;
  scale = m.lossyScale;
}

Both Matrix4x4.rotation and Matrix4x4.lossyScale are undisclosed, so I couldn't investigate how they work.

Before going on I had to freshen it up my linear algebra theory and picked up Foundations of Game Engine Development, Volume 1: Mathematics by Eric Lengyel (great book!) and found some useful inputs. It was immensely helpful when trying to understand other people's code.

There are many different ways to decompose a matrix. I found some algorithms and tried one of them out. Still the same error, but identical (which is also a great observation). I now had a starting point to compare to. Unfortunately I discarded this interim result and cannot find the source anymore.

The next thought was "What does Blender do different than this Unity script?". Since Blender is open source it only seemed natural to me to look it up. Turns out Blender does an additional negativity check on the rotation matrix and flips both scale and rotation in some cases. Sounds exactly like what it's missing, so I decided to port this code and use the Unity.Mathematics package for it. It already contains types and methods I'd need (like float3x3, a 3-by-3 matrix), which saved a lot of time. It's also said to be well optimized, so yay.

Behold the results:

"3D scene showing a car in Unity with correct rotations on all objects"

"Transform component of the tire object in Unity"

🎉🚙😎

Performance

Whilst at it, I ran the conversions in a loop to see how they perform:

"Screenshot of Unity Profiler showing timings and memory consumptions"

So the downside of the correct solution (Matrix4x4.DecomposeCustom) is that it's ~2.3 times slower. This is done once per node. The typical scene won't have a large number of nodes, so it's safe to neglect the minor performance loss.

There's also a tiny raise of memory allocations. I made another, pure Unity.Mathematics types based variant (float4x4.Decompose), which does eliminate this flaw. Another good reason to switch to Unity.Mathematics types overall.

Problem Definition

The original problem turned out to be a corner-case matrix with…

Separating rotation and scale is a non-trivial problem that only gets harder if you cannot assume that the scale is positive. I assume Unity's Matrix4x4.rotation and Matrix4x4.lossyScale was written with only positive scales in mind. It's also worth mentioning that they are two separate, non-coherent calculations (hidden behind properties). It may be, that they're not consistently aligned for corner-cases.

Solution

The solution was to port the matrix decomposition algorithm of Blender to C#:

Here's the Solution Source Code in C# ✅

It can be used like so:

// Given this matrix
Matrix4x4 m;
// But could also be this Unity.Mathematics type
float4x4 m;

m.Decompose(out var t, out var r, out var s);
position = t;
rotation = r;
scale = s;

I hope that was helpful.